（本小题10分）（1）如图①，在凹四边形ABCD中，∠BDC=125°，∠B=∠C=30°，
则∠A = °；
（2）如图②，在凹四边形ABCD中，∠ABD与∠ACD的角平分线交于点E，∠A=60°，∠BDC=140°，
则∠E= °；
（3）如图③，∠ABD，∠BAC的角平分线交于点E，∠C=40°，∠BDC=150°，求∠AEB的度数；
（4）如图④，∠BAC，∠BDC的角平分线交于点E，猜想∠B，∠C与∠E之间有怎样的数量关系，并证明你的猜想．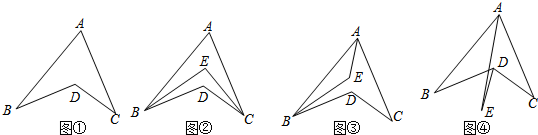
相关试题
(7分)如图，在平面直角坐标中，以点M
为圆心，以
长为半经作圆M交
轴于A，B两点，连结AM并延长交圆M于点P，连结PC交轴于点E。
（1）求点A，C的坐标
（2）求证：BE=2OE
如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交AB于点F，∠ADC的平分线DG交边AB于点G．
（1）求证：AF=GB；
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形，并说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号