[探究发现]如图①，已知△ABC是等边三角形，∠AEF＝60°，EF交等边三角形外角平分线于点F，当点E是BC的中点时，有AE＝EF成立．
[数学思考]某数学兴趣小组在探究AE与EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：
当点E是直线BC上(B，C除外)任意一点时(其他条件不变)，结论AE＝EF仍然成立．
假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在图②中画出图形，并证明AE＝EF．
[拓展应用]当点E在线段BC的延长线上时，若CE＝BC，在图③中画出图形，并运用上述结论求出S△ABC︰S△AEF的值．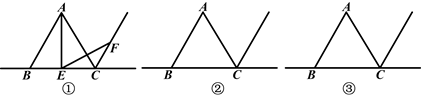
祥云桥位于省城太原南部，该桥塔主体由三根曲线塔柱组合而成，全桥共设13对直线型斜拉索，造型新颖，是“三晋大地”的一种象征．某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动，他们制订了测量方案，并利用课余时间借助该桥斜拉索完成了实地测量．测量结果如下表．
项目 |
内容 |
||
课题 |
测量斜拉索顶端到桥面的距离 |
||
测量示意图 |
|
说明：两侧最长斜拉索 |
|
测量数据 |
|
|
|
234米 |
|||
（1）请帮助该小组根据上表中的测量数据，求斜拉索顶端点到
的距离（参考数据：
，
，
，
，
，
（2）该小组要写出一份完整的课题活动报告，除上表的项目外，你认为还需要补充哪些项目（写出一个即可）．
在“优秀传统文化进校园”活动中，学校计划每周二下午第三节课时间开展此项活动，拟开展活动项目为：剪纸，武术，书法，器乐，要求七年级学生人人参加，并且每人只能参加其中一项活动．教务处在该校七年级学生中随机抽取了100名学生进行调查，并对此进行统计，绘制了如图所示的条形统计图和扇形统计图（均不完整）．
请解答下列问题：
（1）请补全条形统计图和扇形统计图；
（2）在参加“剪纸”活动项目的学生中，男生所占的百分比是多少？
（3）若该校七年级学生共有500人，请估计其中参加“书法”项目活动的有多少人？
（4）学校教务处要从这些被调查的女生中，随机抽取一人了解具体情况，那么正好抽到参加“器乐”活动项目的女生的概率是多少？
如图，一次函数的图象分别与
轴，
轴相交于点
，
，与反比例函数
的图象相交于点
，
．
（1）求一次函数和反比例函数的表达式；
（2）当为何值时，
；
（3）当为何值时，
，请直接写出
的取值范围．
如图，抛物线与
轴交于
、
两点（点
在点
的左侧），与
轴交于点
，连接
、
．点
沿
以每秒1个单位长度的速度由点
向点
运动，同时，点
沿
以每秒2个单位长度的速度由点
向点
运动，当一个点停止运动时，另一个点也随之停止运动，连接
．过点
作
轴，与抛物线交于点
，与
交于点
，连接
，与
交于点
．设点
的运动时间为
秒
．
（1）求直线的函数表达式；
（2）①直接写出，
两点的坐标（用含
的代数式表示，结果需化简）
②在点、
运动的过程中，当
时，求
的值；
（3）试探究在点，
运动的过程中，是否存在某一时刻，使得点
为
的中点？若存在，请直接写出此时
的值与点
的坐标；若不存在，请说明理由．
综合与实践
背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为的三角形称为
，4，
型三角形，例如：三边长分别为9，12，15或
，
，
的三角形就是
，4，
型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．
实践操作 如图1，在矩形纸片中，
，
．
第一步：如图2，将图1中的矩形纸片沿过点
的直线折叠，使点
落在
上的点
处，折痕为
，再沿
折叠，然后把纸片展平．
第二步：如图3，将图2中的矩形纸片再次折叠，使点与点
重合，折痕为
，然后展平，隐去
．
第三步：如图4，将图3中的矩形纸片沿折叠，得到△
，再沿
折叠，折痕为
，
与折痕
交于点
，然后展平．
问题解决
（1）请在图2中证明四边形是正方形．
（2）请在图4中判断与
的数量关系，并加以证明；
（3）请在图4中证明，4，
型三角形；
探索发现
（4）在不添加字母的情况下，图4中还有哪些三角形是，4，
型三角形？请找出并直接写出它们的名称．
粤公网安备 44130202000953号