数学课上,年轻的刘老师在讲授“轴对称”时,设计了如下四种教学方法:
①教师讲,学生听;
②教师让学生自己做;
③教师引导学生画图,发现规律;
④教师让学生对折纸,观察发现规律,然后画图.
数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种,他随机抽取了60名学生的调查问卷,统计如图:
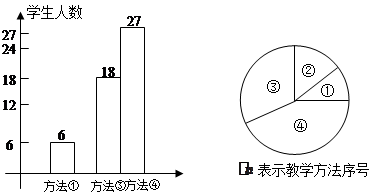
(1)请将条形统计图补充完整,并计算扇形统计图中方法③的圆心角.
(2)全年级同学中最喜欢的教学方法是哪一种?选择这种教学方法的约有多少人?
(3)假如抽取的60名学生集中在某两个班,这个调查结果还合理吗?为什么?
(4)请你对老师的教学方法提出一条合理化的建议.