有下列命题：
①乘积
展开式的项数是24；
②由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是36；
③某会议室第一排共有8个座位，现有3人就座，若要求每人左右均有空位，那么不同的坐法种数为24；
④已知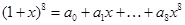
，其中
中奇数的个数为2。
其中真命题的序号是 ．
，则
”的逆否命题为_________
表示一个圆。（1）
的取值范围 ．（2）
的取值范围 ．
上的点到直线
的距离的最小值 ．
过原点的充要条件是 ．
时，两条直线
、
的交点在 象限．推荐套卷
有下列命题：
①乘积展开式的项数是24；
②由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是36；
③某会议室第一排共有8个座位，现有3人就座，若要求每人左右均有空位，那么不同的坐法种数为24；
④已知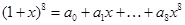，其中中奇数的个数为2。
其中真命题的序号是 ．
粤公网安备 44130202000953号