端午节吃粽子是中华民族的传统习惯.小祥的妈妈从超市买了一些粽子回家,
用不透明袋子装着这些粽子(粽子除内部馅料不同外,其他一切相同),小祥问买了什么样的粽子,妈妈说:
“其中香肠馅粽子两个,剩余的都是绿豆馅粽子,若你从中任意拿出一个是香肠馅粽子的概率为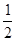 ”.
”.
(1)袋子中绿豆馅粽子有 个;
(2)小祥第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树状图或列表法,求小祥两次拿到的都是绿豆馅粽子的概率.
相关知识点
推荐套卷
端午节吃粽子是中华民族的传统习惯.小祥的妈妈从超市买了一些粽子回家,
用不透明袋子装着这些粽子(粽子除内部馅料不同外,其他一切相同),小祥问买了什么样的粽子,妈妈说:
“其中香肠馅粽子两个,剩余的都是绿豆馅粽子,若你从中任意拿出一个是香肠馅粽子的概率为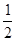 ”.
”.
(1)袋子中绿豆馅粽子有 个;
(2)小祥第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树状图或列表法,求小祥两次拿到的都是绿豆馅粽子的概率.