（本小题9分）如图，P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．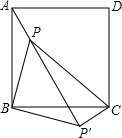
（1）旋转中心是点 ______，点P旋转的度数是______；
（2）连接PP′，△BPP′的形状是 ______三角形；
（3）若PA=2，PB=4，∠APB=135°．
①求△BPP′的周长； ②求PC的长．
值：
，其中 
, 
.
．求A―2B的值，其中
．
）+(-6)2×(-
)2-(
)2×(-8)2］.
推荐套卷
（本小题9分）如图，P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．
（1）旋转中心是点 ______，点P旋转的度数是______；
（2）连接PP′，△BPP′的形状是 ______三角形；
（3）若PA=2，PB=4，∠APB=135°．
①求△BPP′的周长； ②求PC的长．
粤公网安备 44130202000953号