如图,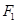 、
、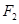 为椭圆
为椭圆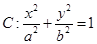 的左、右焦点,
的左、右焦点,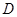 、
、 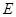 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率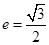 ,
,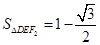 .若
.若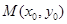 在椭圆
在椭圆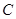 上,则点
上,则点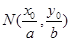 称为点
称为点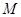 的一个“好点”.直线
的一个“好点”.直线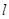 与椭圆交于
与椭圆交于 、
、 两点,
两点,  、
、 两点的“好点”分别为
两点的“好点”分别为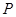 、
、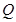 ,已知以
,已知以 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.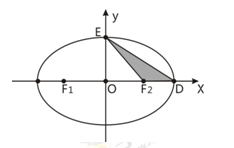
(Ⅰ)求椭圆的标准方程;
(Ⅱ) 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
推荐套卷
如图,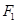 、
、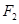 为椭圆
为椭圆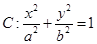 的左、右焦点,
的左、右焦点,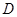 、
、 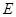 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率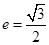 ,
,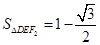 .若
.若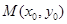 在椭圆
在椭圆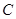 上,则点
上,则点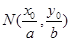 称为点
称为点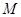 的一个“好点”.直线
的一个“好点”.直线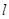 与椭圆交于
与椭圆交于 、
、 两点,
两点,  、
、 两点的“好点”分别为
两点的“好点”分别为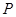 、
、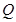 ,已知以
,已知以 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ) 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.