(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是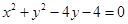 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.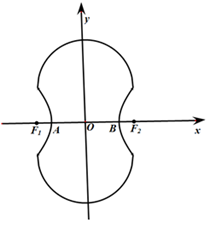
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为 、
、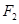 ,试在“8”字形 曲线上求点
,试在“8”字形 曲线上求点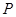 ,使得
,使得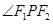 是直角.
是直角.
(3)过点 作直线
作直线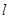 分别交“8”字形曲线中上、下两个半圆于点
分别交“8”字形曲线中上、下两个半圆于点 ,求
,求 的最大长度.
的最大长度.
相关知识点
推荐套卷
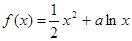 (a∈R).
(a∈R).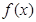 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;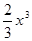 .
. 是二次函数,方程
是二次函数,方程 有两个相等的实根,且
有两个相等的实根,且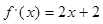 。
。 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把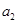 . 对
. 对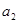 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数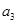 . 当
. 当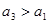 时, 甲获胜, 否则乙获胜. 若甲获胜的概率为
时, 甲获胜, 否则乙获胜. 若甲获胜的概率为 , 求
, 求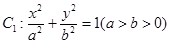 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,椭圆
的焦点重合,椭圆 与抛物线
与抛物线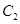 在第一象限的交点为
在第一象限的交点为 ,
, ,求椭圆
,求椭圆 粤公网安备 44130202000953号
粤公网安备 44130202000953号