已知一次函数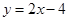
的图像与
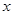轴、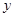
轴分别相交于点A、B，点P在该函数图像上， P到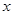轴、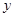轴的距离分别为
、
。
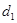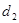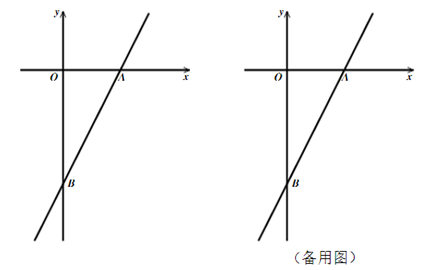
（1）当P为线段AB的中点时，求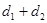
的值；
（2）直接写出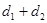的范围，并求当
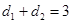时点P的坐标；
（3）若在线段AB 上存在无数个P点，使
（
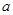为常数）， 求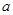的值.
，
，
，
．
． 
； 
．相关知识点
推荐套卷
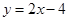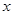已知一次函数的图像与 轴、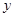轴分别相交于点A、B，点P在该函数图像上， P到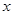轴、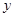轴的距离分别为、。
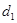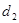（1）当P为线段AB的中点时，求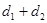的值；
（2）直接写出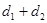的范围，并求当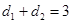时点P的坐标；
（3）若在线段AB 上存在无数个P点，使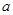（为常数）， 求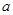的值.
粤公网安备 44130202000953号