已知二次函数f（x）=ax2+bx+c ．
（1） 设集合A={x|f（x）=x}．
①若A={1，2}，且f（0）=2，求f（x）的解析式；
②若A={1}，且a≥1，求f（x）在区间[﹣2，2]上的最大值M（a）．
（2） 设f（x）的图像与x轴有两个不同的交点，a>0， f（c）=0，且当0<x<c时，f（x）>0．用反证法证明：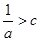
．
相关试题
中，
，
.
；
，求
，且
，求
b的值.
的图象与直线
相切，并且切点的横坐标依次成公差
的等差数列。
的值；
是
图象的对称中心，且
,求点
的坐标。
的值；
中，
，
，
，
记
，
关于
的表达式；推荐套卷
已知二次函数f（x）=ax2+bx+c ．
（1） 设集合A={x|f（x）=x}．
①若A={1，2}，且f（0）=2，求f（x）的解析式；
②若A={1}，且a≥1，求f（x）在区间[﹣2，2]上的最大值M（a）．
（2） 设f（x）的图像与x轴有两个不同的交点，a>0， f（c）=0，且当0<x<c时，f（x）>0．用反证法证明：．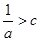
粤公网安备 44130202000953号