如图，已知直线y＝－
x＋2与坐标轴交于A、B两点，抛物线y＝－
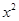＋bx＋c与x轴交于A、C两点，与y轴交于点B．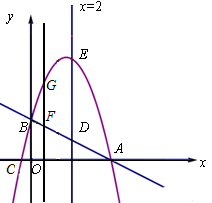
（1）求b、c的值．
（2）平行于y轴的直线x＝2交直线AB于点D，交抛物线于点E．
①点P从原点O出发，沿x轴正方向以1个单位/秒的速度运动，设运动时间为t，过点P作x轴的垂线与直线AB交于点F，与抛物线交于点G，当t为何值时，FG∶DE＝1∶2？
②将抛物线向上平移m（m＞0）个单位后与y轴相交于点B′，与直线x＝2相交于点E′，当E′O平分∠B′E′D时，求m的值．
相关试题
（广安）数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度，如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α，已知tanα=
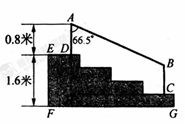
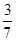，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．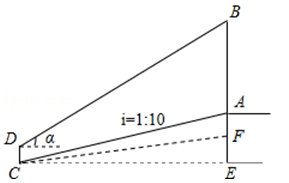
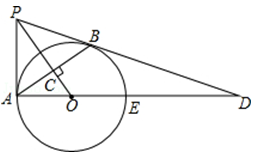
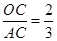（广安）如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
（1）求证：PA是⊙O的切线；
（2）若
，且OC=4，求PA的长和tanD的值．
．
相关知识点
推荐套卷
粤公网安备 44130202000953号