(本小题满分13分)从万州二中高二年级文科学生中随机抽取60名学生,将其月考的政治成绩(均为整数)分成六段:  ,
,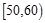 ,…,
,…,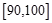 后得到如下频率分布直方图 .
后得到如下频率分布直方图 .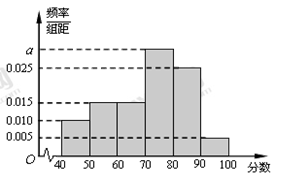
(Ⅰ)求分数在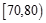 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率.
推荐套卷
(本小题满分13分)从万州二中高二年级文科学生中随机抽取60名学生,将其月考的政治成绩(均为整数)分成六段:  ,
,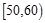 ,…,
,…,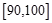 后得到如下频率分布直方图 .
后得到如下频率分布直方图 .
(Ⅰ)求分数在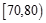 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率.