在平面直角坐标系xOy中,抛物线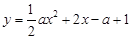 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为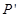 ,求点
,求点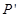 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(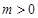 )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线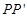 无交点,求m的取值范围.
无交点,求m的取值范围.
相关知识点
推荐套卷
在平面直角坐标系xOy中,抛物线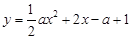 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为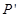 ,求点
,求点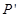 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(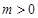 )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线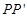 无交点,求m的取值范围.
无交点,求m的取值范围.