如图，已知△ABC．按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结BD，与AC交于点E，连结AD，CD．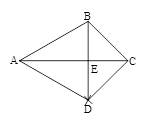
（1）求证：△ABC≌△ADC；
（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．
相关试题
．
的值．
＝0，求方程ax＋
＝7的解．
相关知识点
推荐套卷
如图，已知△ABC．按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结BD，与AC交于点E，连结AD，CD．
（1）求证：△ABC≌△ADC；
（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．
粤公网安备 44130202000953号