在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
相关知识点
推荐套卷
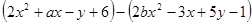 的值与字母x所取的值无关,试求代数式
的值与字母x所取的值无关,试求代数式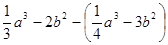 的值.
的值.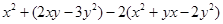 ,其中
,其中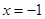 ,
,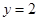 .
.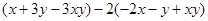 ,其中
,其中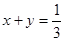 ,
,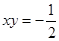 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号