如图，设椭圆
（a＞b＞0）的右焦点为F（1，0），A为椭圆的上顶点，椭圆上的点到右焦点的最短距离为
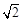
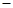1．过F作椭圆的弦PQ，直线AP，AQ分别交直线x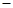y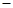2＝0于点M，N．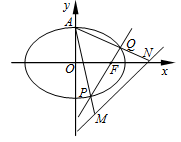
（Ⅰ）求椭圆的方程；
（Ⅱ）求当|MN|最小时直线PQ的方程．
，求点Q的轨迹方程，并说明轨迹是什么曲线。
推荐套卷
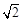
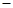如图，设椭圆 （a＞b＞0）的右焦点为F（1，0），A为椭圆的上顶点，椭圆上的点到右焦点的最短距离为1．过F作椭圆的弦PQ，直线AP，AQ分别交直线x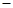y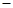2＝0于点M，N．
（Ⅰ）求椭圆的方程；
（Ⅱ）求当|MN|最小时直线PQ的方程．
粤公网安备 44130202000953号