(本小题满分13分)如图,直角坐标系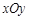 中,一直角三角形
中,一直角三角形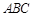 ,
,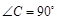 ,
,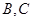 在
在 轴上且关于原点
轴上且关于原点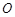 对称,
对称,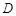 在边
在边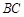 上,
上,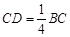 ,
,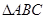 的周长为12.若一双曲线
的周长为12.若一双曲线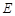 以
以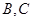 为焦点,且经过
为焦点,且经过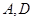 两点.
两点.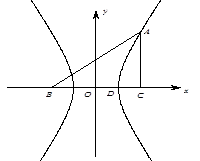
(1)求双曲线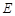 的方程;
的方程;
(2)若一过点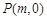 (
(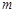 为非零常数)的直线
为非零常数)的直线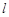 与双曲线
与双曲线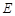 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点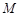 、
、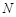 ,且
,且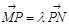 ,问在
,问在 轴上是否存在定点
轴上是否存在定点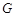 ,使
,使 ?若存在,求出所有这样定点
?若存在,求出所有这样定点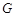 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
(本小题满分13分)如图,直角坐标系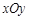 中,一直角三角形
中,一直角三角形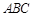 ,
,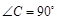 ,
,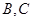 在
在 轴上且关于原点
轴上且关于原点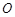 对称,
对称,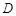 在边
在边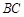 上,
上,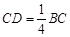 ,
,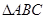 的周长为12.若一双曲线
的周长为12.若一双曲线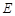 以
以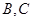 为焦点,且经过
为焦点,且经过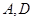 两点.
两点.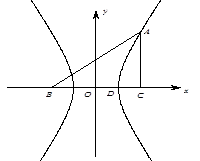
(1)求双曲线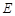 的方程;
的方程;
(2)若一过点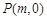 (
(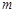 为非零常数)的直线
为非零常数)的直线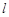 与双曲线
与双曲线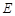 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点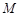 、
、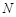 ,且
,且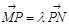 ,问在
,问在 轴上是否存在定点
轴上是否存在定点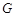 ,使
,使 ?若存在,求出所有这样定点
?若存在,求出所有这样定点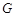 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.