如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).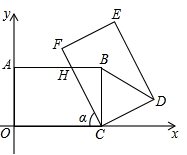
(1)当α=60°时,△CBD的形状是 .
(2)当AH=HC时,求直线FC的解析式.
相关知识点
推荐套卷
如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).
(1)当α=60°时,△CBD的形状是 .
(2)当AH=HC时,求直线FC的解析式.