在菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.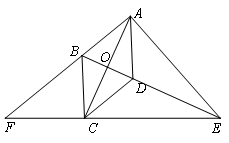
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
相关知识点
推荐套卷
在菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.