(本题满分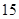 分)已知抛物线
分)已知抛物线 :
: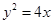 ,过
,过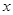 轴上的一定点
轴上的一定点 的直线
的直线 交抛物线
交抛物线 于
于 、
、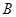 两点(
两点( 为大于零的正常数).
为大于零的正常数).
(1)设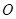 为坐标原点,求
为坐标原点,求 面积的最小值;
面积的最小值;
(2)若点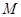 为直线
为直线 上任意一点,探求:直线
上任意一点,探求:直线 的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.
的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.
相关知识点
推荐套卷
(本题满分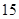 分)已知抛物线
分)已知抛物线 :
: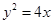 ,过
,过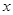 轴上的一定点
轴上的一定点 的直线
的直线 交抛物线
交抛物线 于
于 、
、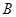 两点(
两点( 为大于零的正常数).
为大于零的正常数).
(1)设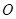 为坐标原点,求
为坐标原点,求 面积的最小值;
面积的最小值;
(2)若点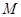 为直线
为直线 上任意一点,探求:直线
上任意一点,探求:直线 的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.
的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.