问题情境:用同样大小的黑色棋子按如图所示的规律摆放,则第2012个图共有多少枚棋子?
建立模型:有些规律问题可以借助函数思想来探讨,具体步骤:第一步,确定变量;第二步,在直角坐标系中画出函数图象;第三步,根据函数图象猜想并求出函数关系式;第四步,把另外的某一点代入验证,若成立,则用这个关系式去求解.
解决问题:根据以上步骤,请你解答“问题情境”.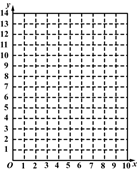
问题情境:用同样大小的黑色棋子按如图所示的规律摆放,则第2012个图共有多少枚棋子?
建立模型:有些规律问题可以借助函数思想来探讨,具体步骤:第一步,确定变量;第二步,在直角坐标系中画出函数图象;第三步,根据函数图象猜想并求出函数关系式;第四步,把另外的某一点代入验证,若成立,则用这个关系式去求解.
解决问题:根据以上步骤,请你解答“问题情境”.