(本小题满分12分)从一批草莓中,随机抽取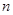 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
| 分组(重量) |
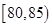 |
 |
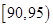 |
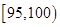 |
| 频数(个) |
 |
 |
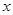 |
 |
已知从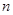 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在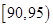 的草莓的概率为
的草莓的概率为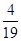 .
.
(1)求出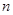 ,
,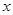 的值;
的值;
(2)用分层抽样的方法从重量在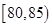 和
和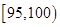 的草莓中共抽取
的草莓中共抽取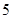 个,再从这
个,再从这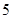 个草莓中任取
个草莓中任取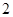 个,求重量在
个,求重量在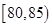 和
和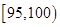 中各有
中各有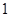 个的概率.
个的概率.
推荐套卷
(本小题满分12分)从一批草莓中,随机抽取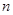 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
| 分组(重量) |
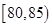 |
 |
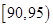 |
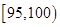 |
| 频数(个) |
 |
 |
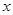 |
 |
已知从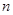 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在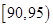 的草莓的概率为
的草莓的概率为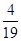 .
.
(1)求出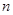 ,
,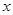 的值;
的值;
(2)用分层抽样的方法从重量在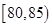 和
和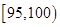 的草莓中共抽取
的草莓中共抽取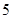 个,再从这
个,再从这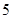 个草莓中任取
个草莓中任取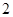 个,求重量在
个,求重量在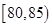 和
和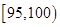 中各有
中各有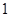 个的概率.
个的概率.