对于定义域为
的函数
,若存在正常数
,使得
是以
为周期的函数,则称
为余弦周期函数,且称
为其余弦周期.已知
是以
为余弦周期的余弦周期函数,其值域为 .设
单调递增,
,
.
.设
单调递增,
,
.
(1)验证
是以
为周期的余弦周期函数;
(2)设
.证明对任意
,存在
,使得
;
(3)证明:"
为
在
上得解"的充要条件是"
为方程
在
上有解",并证明对任意
都有
.
相关知识点
推荐套卷
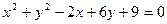
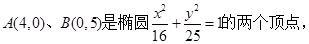 C是椭圆上不同于A、B的点,求三角形ABC面积的最大值。
C是椭圆上不同于A、B的点,求三角形ABC面积的最大值。


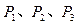 到焦点F2的距离也成等差数列。
到焦点F2的距离也成等差数列。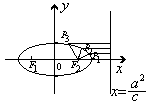
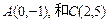
 粤公网安备 44130202000953号
粤公网安备 44130202000953号