当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A.基本不用;B,平均一天使用1—2小时;C.平均一天使用2—4小时;D.平均一天使用4—6小时:E.平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图,请根据相关信息,
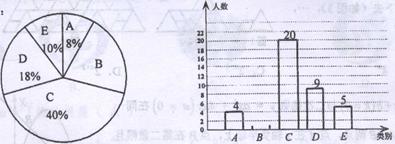
解答下列问题
(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间趣过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”:
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.