（本题5分）如下图，在每个小正方形边长为1的方格纸中， △ABC的顶点都在方格纸格点上．
（1）△ABC的面积为 ；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B'，补全△A′B′C′；
（3）若连接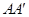
，
，则这两条线段之间的关系是 ；
（4）在图中画出△ABC的高CD；
（5）能使S△ABC＝S△QBC的格点Q，共有 个．
相关试题
则 ①当
取什么值时，方程有两个不相等的实数根？②当
ABCD，四个内角平分线相交于E、F、G、H。求证：四边形EFGH是矩形。
；
取何值时是一元二次方程，并求出此方程的解；
推荐套卷
（本题5分）如下图，在每个小正方形边长为1的方格纸中， △ABC的顶点都在方格纸格点上．
（1）△ABC的面积为 ；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B'，补全△A′B′C′；
（3）若连接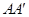，，则这两条线段之间的关系是 ；
（4）在图中画出△ABC的高CD；
（5）能使S△ABC＝S△QBC的格点Q，共有 个．
粤公网安备 44130202000953号