如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连接DE并延长交射线AB于点F，连接BE．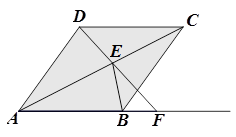
（1）求证：∠AFD=∠EBC ；
（2）是否存在这样一个菱形，当DE＝EC时，刚好BE⊥AF？若存在，求出∠DAB的度数，若不存在，请说明理由 ；
（3）若∠DAB＝90°，且当△BEF为等腰三角形时，求∠EFB的度数．
如图，在平面直角坐标系中，抛物线
与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为（-1，0），（0，-2），点D在
轴上且AD为⊙M的直径。点E是⊙M与
轴的另一个交点，过劣弧
上的点F作FH⊥AD于点H，且FH=1．5。
（1）求点D的坐标及该抛物线的表达式；
（2）若点P是轴上的一个动点，试求出⊿PEF的周长最小时点P的坐标；
（3）在抛物线的对称轴上是否存在点Q，使⊿QCM是等腰三角形？如果存在，请直接写出点Q的坐标；如果不存在，请说明理由。
如图1，直线y=k1x与反比例函数y=
（k≠0）的图象交于点A，B，直线y=k2x与反比例函数y=的图象交于点C，D，且k1•k2≠0，k1≠k2，顺次连接A，D，B，C，AD，BC分别交x轴于点F，H，交y轴于点E，G，连接FG，EH．
（1）四边形ADBC的形状是 ；
（2）如图2，若点A的坐标为（2，4），四边形AEHC是正方形，则k2= ；
（3）如图3，若四边形EFGH为正方形，点A的坐标为（2，6），求点C的坐标；
（4）判断：随着k1、k2取值的变化，四边形ADBC能否为正方形？若能，求点A的坐标；若不能，请简要说明理由．
如图，平行四边形ABCD中，BD⊥AD，∠A=45°，E，F分别是AB，CD上的点，且BE=DF，连接EF∠BD于O．
（1）求证：BO=DO
（2）若EF⊥AB，延长EF∠AD的延长线于G，当FG=1时，求AD的长．
B
B
粤公网安备 44130202000953号