（本题8分）仪征市某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力．小华与小明同学就“最喜欢哪种学习方式” 随机调查了他们周围的一些同学，根据收集到的数据绘制了以下的两个统计图．请根据下面两个不完整的统计图回答以下问题：
（1）这次抽样调查中，共调查了 名学生；
（2）补全两幅统计图；
（3）根据抽样调查的结果，估算该校1000名学生中大约有多少人选择“小组合作学习”？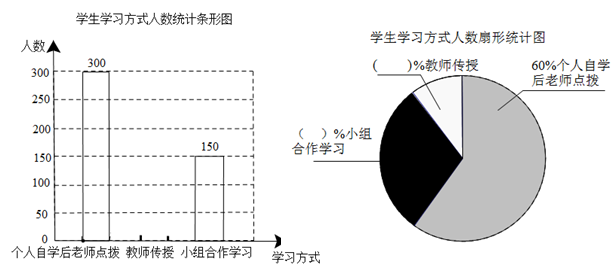
相关试题
已知抛物线y＝－x2＋2x＋2．
（1）该抛物线的对称轴是 ，顶点坐标 ；
（2）选取适当的数据填入下表，并在下图的直角坐标系内描点画出该抛物线的图象；
| x |
… |
… |
|||||
| y |
… |
… |
（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足x1＞x2＞1，试比较y1与y2的大小．
，AD＝2．问当AB的长为多少时，这两个直角三角形相似？
如图，一个二次函数的图象经过点A、C、B三点，点A的坐标为（
），点B的坐标为（3,0），点C在y轴的正半轴上，且AB=OC．
（1）求点C的坐标；
（2）求这个二次函数的解析式，并求出该函数的最大值．
已知二次函数y=-0．5x2+4x-3．5
（1）用配方法把该函数化为y=a(x-h)2+k的形式,并指出函数图象的对称轴和顶点坐标；
（2）求函数图象与x轴的交点坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号