如图1, ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.
ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.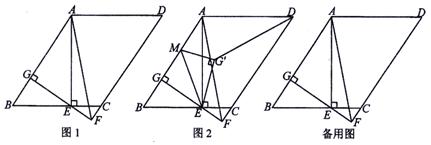
(1)若BE=2EC,AB =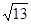 ,求AD的长;
,求AD的长;
(2)求证:EG=BG+FC;
(3)如图2,若AF=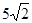 ,EF=2,点
,EF=2,点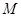 是线段 AG上的一个动点,连接
是线段 AG上的一个动点,连接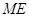 ,将
,将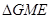 沿
沿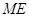 翻折得
翻折得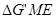 ,连接
,连接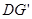 ,试求当
,试求当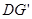 取得最小值时
取得最小值时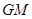 的长.
的长.
相关知识点
推荐套卷
如图1, ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.
ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.
(1)若BE=2EC,AB =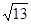 ,求AD的长;
,求AD的长;
(2)求证:EG=BG+FC;
(3)如图2,若AF=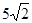 ,EF=2,点
,EF=2,点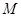 是线段 AG上的一个动点,连接
是线段 AG上的一个动点,连接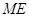 ,将
,将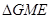 沿
沿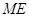 翻折得
翻折得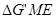 ,连接
,连接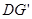 ,试求当
,试求当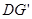 取得最小值时
取得最小值时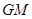 的长.
的长.