某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=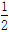 x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
(1)试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入-购进成本)