如图,已知矩形ABCD,AB=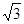 ,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.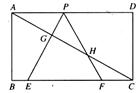
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形 (不含全等形),并证明;
(3)若△PEF的边EF在线段BC上以每秒1个单位的速度移动.设BE的长为 ,PH的长为
,PH的长为 ,请你写出
,请你写出 与
与 的函数式,并指出函数自变量的取值范围.
的函数式,并指出函数自变量的取值范围.
相关知识点
推荐套卷
如图,已知矩形ABCD,AB=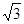 ,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形 (不含全等形),并证明;
(3)若△PEF的边EF在线段BC上以每秒1个单位的速度移动.设BE的长为 ,PH的长为
,PH的长为 ,请你写出
,请你写出 与
与 的函数式,并指出函数自变量的取值范围.
的函数式,并指出函数自变量的取值范围.