已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.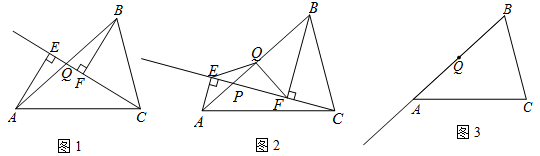
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
相关知识点
推荐套卷
已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.