(本小题14分)
已知函数f(x)=ax3+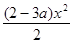 +bx(a,b为常数)
+bx(a,b为常数)
1) 若y=f(x)的图象在x=2处的切线方程为x-y+6=0,求函数y=f(x)的解析式;
2) 在1)的条件下,讨论函数y=f(x)的图象与函数y =- [f /(x)-9x-3]+m的图象的交点的个数;
[f /(x)-9x-3]+m的图象的交点的个数;
3) 当a=1时, ,lnx ≤f /(x)恒成立,求实数b的取值范围。
,lnx ≤f /(x)恒成立,求实数b的取值范围。
推荐套卷
(本小题14分)
已知函数f(x)=ax3+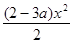 +bx(a,b为常数)
+bx(a,b为常数)
1) 若y=f(x)的图象在x=2处的切线方程为x-y+6=0,求函数y=f(x)的解析式;
2) 在1)的条件下,讨论函数y=f(x)的图象与函数y =- [f /(x)-9x-3]+m的图象的交点的个数;
[f /(x)-9x-3]+m的图象的交点的个数;
3) 当a=1时, ,lnx ≤f /(x)恒成立,求实数b的取值范围。
,lnx ≤f /(x)恒成立,求实数b的取值范围。