某校九年级（1）班所有学生参加2015年初中毕业生升学体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：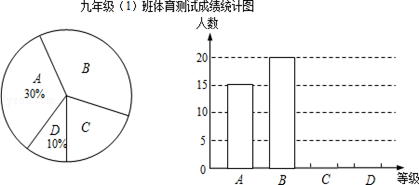
（1）九年级（1）班参加体育测试的学生有 人；
（2）将条形统计图补充完整；
（3）在扇形统计图中，等级B部分所占的百分比是 ，等级C对应的圆心角的度数为 ；
（4）若该校九年级学生共有850人参加体育测试，估计达到A级和B级的学生共有 人．
相关试题
为庆祝中国共产党成立100周年，某校计划举行“学党史 感党恩”知识竞答活动，并计划购置篮球、钢笔、笔记本作为奖品．采购员刘老师在某文体用品店购买了做为奖品的三种物品，回到学校后发现发票被弄花了，有几个数据变得不清楚，如图．
请根据图所示的发票中的信息，帮助刘老师复原弄花的数据，即分别求出购置钢笔、笔记本的数量及对应的金额．
相关知识点
推荐套卷
粤公网安备 44130202000953号