如图，直线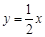
与双曲线
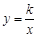（k＞0，x＞0）交于点A，将直线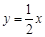向上平移4个单位长度后，与y轴交于点C，与双曲线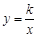（k＞0，x＞0）交于点B．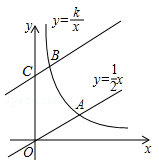
（1）设点B的横坐标分别为b，试用只含有字母b 的代数式表示k；
（2）若OA=3BC，求k的值．
，其中
．
，
，求
．
， 
，
．
，
，
，
，
相关知识点
推荐套卷
如图，直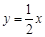线与双曲线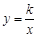（k＞0，x＞0）交于点A，将直线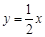向上平移4个单位长度后，与y轴交于点C，与双曲线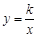（k＞0，x＞0）交于点B．
（1）设点B的横坐标分别为b，试用只含有字母b 的代数式表示k；
（2）若OA=3BC，求k的值．
粤公网安备 44130202000953号