如图，在平面直角坐标系中，O为坐标原点，抛物线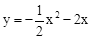
与x轴相交于O、B，顶点为A，连接OA．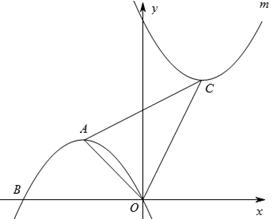
（1）求点A的坐标和∠AOB的度数；
（2）若将抛物线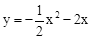向右平移4个单位，再向上平移2个单位，再向上翻转，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；
（3）在（2）的情况下，判断点C′是否在抛物线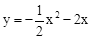上，请说明理由；
如图，在平面直角坐标系中，O为坐标原点，抛物线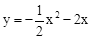与x轴相交于O、B，顶点为A，连接OA．
（1）求点A的坐标和∠AOB的度数；
（2）若将抛物线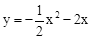向右平移4个单位，再向上平移2个单位，再向上翻转，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；
（3）在（2）的情况下，判断点C′是否在抛物线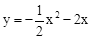上，请说明理由；
（3）－
（4）（－5）3
，即
，即
等于什么，并通过计算验证你的猜想。
= 0。
粤公网安备 44130202000953号