如图①，在矩形纸片ABCD中，AB=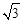
+1，AD=．
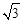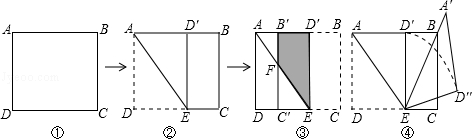
（1）如图②，将矩形纸片向上方翻折，使点D恰好落在AB边上的D′处，压平折痕交CD于点E，则折痕AE的长为 ；
（2）如图③，再将四边形BCED′沿D′E向左翻折，压平后得四边形B′C′ED′，B′C′交AE于点F，则四边形B′FED′的面积为 ；
（3）如图④，将图②中的△AED′绕点E顺时针旋转α角，得△A′ED″，使得EA′恰好经过顶点B，求弧D′D″的长．（结果保留π）
如图①，在矩形纸片ABCD中，AB=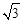+1，AD=．
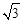（1）如图②，将矩形纸片向上方翻折，使点D恰好落在AB边上的D′处，压平折痕交CD于点E，则折痕AE的长为 ；
（2）如图③，再将四边形BCED′沿D′E向左翻折，压平后得四边形B′C′ED′，B′C′交AE于点F，则四边形B′FED′的面积为 ；
（3）如图④，将图②中的△AED′绕点E顺时针旋转α角，得△A′ED″，使得EA′恰好经过顶点B，求弧D′D″的长．（结果保留π）
，其中x=-
”，小强做题时把“x=-
，其中x=1．
粤公网安备 44130202000953号