如图①,在平面直角坐标系中,已知点A(2,0),点B(0,4),点E(0,1),如图②,将△AEO沿x轴向左平移得到△A′E′O′,连接A′B、BE′。
(1)设AA′=m(m >0),试用含m的式子表示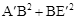 ,并求出使
,并求出使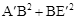 取得最小值时点E′的坐标;
取得最小值时点E′的坐标;
(2)当A′B+BE′取得最小值时,求点E′的坐标。
如图①,在平面直角坐标系中,已知点A(2,0),点B(0,4),点E(0,1),如图②,将△AEO沿x轴向左平移得到△A′E′O′,连接A′B、BE′。
(1)设AA′=m(m >0),试用含m的式子表示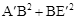 ,并求出使
,并求出使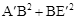 取得最小值时点E′的坐标;
取得最小值时点E′的坐标;
(2)当A′B+BE′取得最小值时,求点E′的坐标。