（年湖北武汉12分）如图，已知直线AB：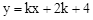
与抛物线
交于A、B两点，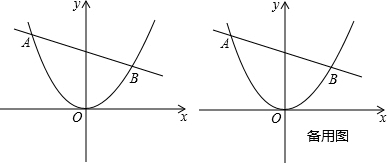
（1）直线AB总经过一个定点C，请直接写出点C坐标；
（2）当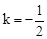
时，在直线AB下方的抛物线上求点P，使△ABP的面积等于5；
（3）若在抛物线上存在定点D使∠ADB＝90°，求点D到直线AB的最大距离.
（年湖北武汉12分）如图，已知直线AB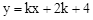：与抛物线交于A、B两点，
（1）直线AB总经过一个定点C，请直接写出点C坐标；
（2）当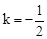时，在直线AB下方的抛物线上求点P，使△ABP的面积等于5；
（3）若在抛物线上存在定点D使∠ADB＝90°，求点D到直线AB的最大距离.
+3x 的值
，
，
，求∠A的度数。
中，A(0,5)，B(-3，2),C(-1,-1)．
关于
轴的对称图形
．
的坐标为．
＋
—
粤公网安备 44130202000953号