（年江苏徐州10分）如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．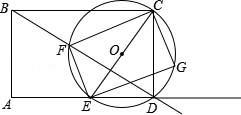
（1）试说明四边形EFCG是矩形；
（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．
相关试题
如图1，在正方形ABCD中，等腰三角形AEF的顶点E，F分别在BC和CD上.
（1）求证：BE=DF；
（2）若等腰三角形AEF的腰AE比正方形ABCD的边AB长1，BE=5，求正方形ABCD的面积；
（3）若∠EAF=50°，则
①如图1，∠BAE=°；
②如图2，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，求∠BAE的大小．
如图，在矩形ABCD中，AC与BD相交于O，∠COD=60°，点E是BC边上的动点，连结DE，OE．
（1）求证：△COD是等边三角形；
（2）如图1，当DE平分∠ADC时，试证明OC=EC，并求出∠DOE的度数；
（3）如图2，当DE平分∠BDC时，试证明
．
如图，在等腰梯形ABCD中，AD∥BC，AB=DC，将腰AB平移至DE的位置时，四边形ABED是平行四边形．
（1）求证：∠C=∠ADE；
（2）若下底BC比上底AD长4cm，DC=3cm，求
的周长．
在同一条直线上，
，
．
．
粤公网安备 44130202000953号