(年广东佛山10分)(1)证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;[要求根据图1写出已知、求证、证明;在证明过程中,至少有两处写出推理依据(“已知”除外)
(2)如图2,在▱ABCD中,对角线焦点为O,A1、B1、C1、D1分别是OA、OB、OC、OD的中点,A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点,…,以此类推.
若ABCD的周长为1,直接用算式表示各四边形的周长之和l;
(3)借助图形3反映的规律,猜猜l可能是多少?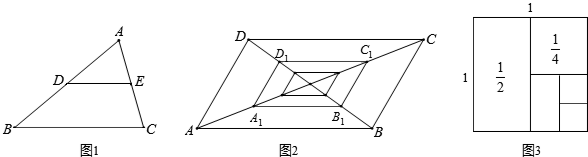
(年广东佛山10分)(1)证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;[要求根据图1写出已知、求证、证明;在证明过程中,至少有两处写出推理依据(“已知”除外)
(2)如图2,在▱ABCD中,对角线焦点为O,A1、B1、C1、D1分别是OA、OB、OC、OD的中点,A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点,…,以此类推.
若ABCD的周长为1,直接用算式表示各四边形的周长之和l;
(3)借助图形3反映的规律,猜猜l可能是多少?