（1）证明：当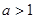
时，不等式
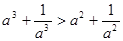成立；
（2）要使上述不等式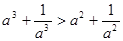成立，能否将条件“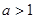”适当放宽？若能，请放宽条件并简述理由；若不能，也请说明理由；
（3）请你根据（1）、（2）的证明，试写出一个类似的更为一般的结论，且给予证明．
相关试题
； 
为何实数
总是增函数；
为奇函数时，求
是定义在R上的偶函数，当
时，
的值；
的解析式并画出简图；
的根的情况。
上是增函数；
在
上的值域。
的值；
的奇偶性。
相关知识点
推荐套卷
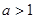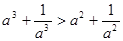（1）证明：当时，不等式成立；
（2）要使上述不等式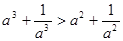成立，能否将条件“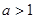”适当放宽？若能，请放宽条件并简述理由；若不能，也请说明理由；
（3）请你根据（1）、（2）的证明，试写出一个类似的更为一般的结论，且给予证明．
粤公网安备 44130202000953号