(本大题满分13分)对于给定数列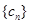 ,如果存在实常数
,如果存在实常数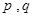 使得
使得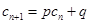 对于任意
对于任意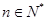 都成立,我们称数列
都成立,我们称数列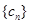 是 “线性数列”.
是 “线性数列”.
(1)若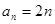 ,
,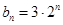 ,
,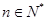 ,数列
,数列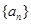 、
、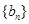 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列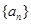 是“线性数列”,则数列
是“线性数列”,则数列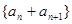 也是“线性数列”;
也是“线性数列”;
(3)若数列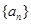 满足
满足 ,
,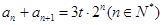 ,
, 为常数.求数列
为常数.求数列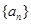 前
前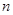 项的和.
项的和.
推荐套卷
(本大题满分13分)对于给定数列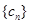 ,如果存在实常数
,如果存在实常数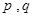 使得
使得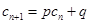 对于任意
对于任意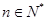 都成立,我们称数列
都成立,我们称数列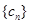 是 “线性数列”.
是 “线性数列”.
(1)若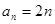 ,
,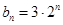 ,
,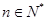 ,数列
,数列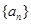 、
、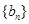 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列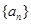 是“线性数列”,则数列
是“线性数列”,则数列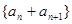 也是“线性数列”;
也是“线性数列”;
(3)若数列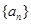 满足
满足 ,
,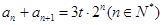 ,
, 为常数.求数列
为常数.求数列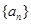 前
前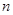 项的和.
项的和.