(本题满分14分)已知抛物线
的焦点为F，点P是抛物线上的一点，且其纵坐标为4，
．
（1）求抛物线的方程；
（2）设点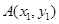
，
（
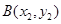）是抛物线上的两点，∠APB的角平分线与x轴垂直，求△PAB的面积最大时直线AB的方程．
的焦点的直线交抛物线与
两点，求
上距
（
最近的点恰好是顶点的充要条件是什么
的焦点
作直线，与抛物线分别交于
两点，
的定义域为{
，且当
时，
的所有
是各棱长为5的正三棱柱，
,
分别是
,
的中点，则平面
与平面
的距离为多少
相关知识点
推荐套卷
(本题满分14分)已知抛物线的焦点为F，点P是抛物线上的一点，且其纵坐标为4，．
（1）求抛物线的方程；
（2）设点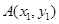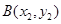，（）是抛物线上的两点，∠APB的角平分线与x轴垂直，求△PAB的面积最大时直线AB的方程．
粤公网安备 44130202000953号