（本小题满分12分）某校从参加某次知识竞赛的同学中，选取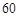
名同学将其成绩（百分制，均为整数）分成
，
，
，
，
，
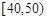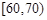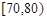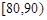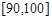六组后，得到频率分布直方图（如图），观察图形中的信息，回答下列问题．
（1）从频率分布直方图中，估计本次考试成绩的中位数；
（2）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．
相关试题
中,侧棱与底面垂直,
,
,点
分别为
和
的中点.
平面
;
的体积;
平面
.
中，角
所对的边分别是
，且
．
的大小；
，
，求
． 
三点共线，求实数
的值；
成立
为正数，求证：
，不等式
的解集为
时，证明：
推荐套卷
（本小题满分12分）某校从参加某次知识竞赛的同学中，选取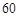名同学将其成绩（百分制，均为整数）分成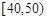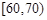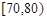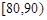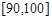，，，，，六组后，得到频率分布直方图（如图），观察图形中的信息，回答下列问题．
（1）从频率分布直方图中，估计本次考试成绩的中位数；
（2）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．
粤公网安备 44130202000953号