如图所示,机器人海宝按照以下程序运行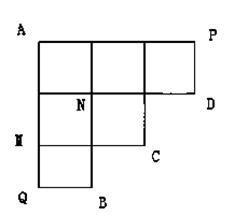
①从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率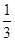 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.
相关知识点
推荐套卷
如图所示,机器人海宝按照以下程序运行
①从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率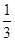 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.