某市现有居民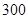 万人,每天有
万人,每天有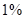 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为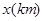 ,
,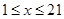 。由调查数据得到
。由调查数据得到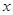 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程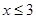 时,乘车费用为
时,乘车费用为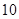 元;当
元;当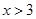 时,每超出
时,每超出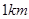 (不足
(不足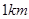 时按
时按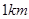 计算),乘车费用增加
计算),乘车费用增加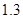 元。
元。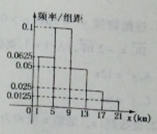
(Ⅰ)求从乘客中任选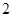 人乘车里程相差超过
人乘车里程相差超过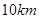 的概率;
的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到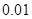 万元)
万元)
推荐套卷
某市现有居民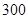 万人,每天有
万人,每天有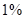 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为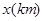 ,
,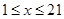 。由调查数据得到
。由调查数据得到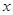 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程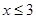 时,乘车费用为
时,乘车费用为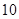 元;当
元;当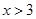 时,每超出
时,每超出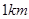 (不足
(不足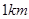 时按
时按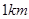 计算),乘车费用增加
计算),乘车费用增加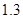 元。
元。
(Ⅰ)求从乘客中任选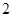 人乘车里程相差超过
人乘车里程相差超过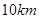 的概率;
的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到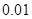 万元)
万元)