已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD
⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．
（Ⅰ）求证：EF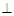
平面PAD；
（Ⅱ）求平面EFG与平面ABCD所成锐二面角的大小；
，
在
处有极值，求a；
上为增函数，求a的取值范围.
的前
项和为
，且满足
．
，
，
，
的值并写出其通项公式；
，试证明
至少有一个不小于1.
是函数f(x)=ln(x+1)-x+
x2的一个极值点。
，则
推荐套卷
已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD
⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．
（Ⅰ）求证：EF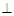平面PAD；
（Ⅱ）求平面EFG与平面ABCD所成锐二面角的大小；
粤公网安备 44130202000953号