一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至 C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向。
(1)求海警船距离事故船C的距离BC.
(2)若海警船以40海里/小时的速度前往救援,求海警船到达事故船C处大约所需的时间.(温馨提示:sin 53°≈0.8,cos 53°≈0.6)
相关知识点
推荐套卷
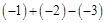 (2)
(2)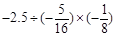
 (4)
(4)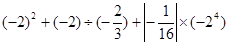

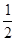 CD。
CD。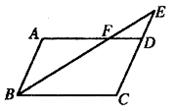
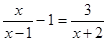 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号