定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.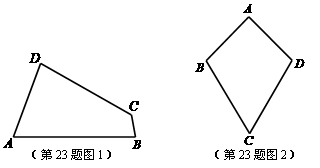
(1)已知:如图1,四边形 是“等对角四边形”,
是“等对角四边形”,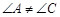 ,
,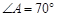 ,
,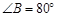 .求
.求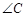 ,
,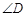 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形” (如图2),其中
(如图2),其中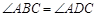 ,
,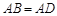 ,此时她发现
,此时她发现 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形” 中,
中,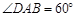 ,
,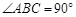 ,
,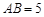 ,
,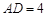 .求对角线
.求对角线 的长.
的长.
相关知识点
推荐套卷


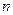 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在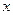 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物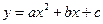
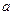 <0)过矩形顶点B、C.
<0)过矩形顶点B、C.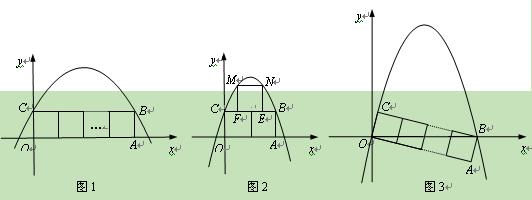
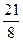 ;
;
 ,cos41°=
,cos41°=

 粤公网安备 44130202000953号
粤公网安备 44130202000953号