(本小题满分10分)我区积极开展“体育大课间”活动,引导学生坚持体育锻炼.某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题: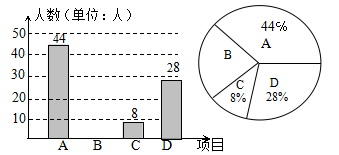
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校最喜欢足球的人数是多少?
相关知识点
推荐套卷
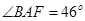 ,
,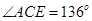 ,
,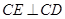 .问
.问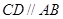 吗?为什么?
吗?为什么?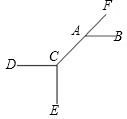

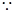
 ,(已知)
,(已知)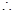
 =
= .( )
.( ) ,(已知)
,(已知) = ,( )
= ,( ) = ;( )
= ;( ) ,
, ,
, .试判断
.试判断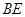 与
与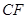 的关系,并说明你的理由.
的关系,并说明你的理由. ,理由是:
,理由是: ,
, .( )
.( ) ,( )
,( ) ,即
,即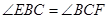 .
. ;(
;( 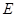 点为
点为 上的点,
上的点, 点为
点为 上的点,
上的点, ,试说明:
,试说明: .
. ,( )
,( ) ,(等量代换)
,(等量代换) ,( )
,( ) ,(已知)
,(已知) ,( )
,( ) .( )
.( ) ,
, ,试说明
,试说明 的理由.
的理由.
 、
、 交于点
交于点 ,
,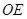 平分
平分 ,若
,若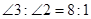 ,
,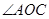 的度数.
的度数.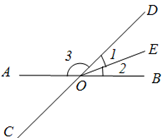

 粤公网安备 44130202000953号
粤公网安备 44130202000953号